vdweller
Member
Hi all,
This is mainly a discussion/presentation of ideas thread. There are lots of good pathfinding concepts and I am not pretending to know all about them. Hopefully this thread will grow to a meaningful exchange of knowledge. I will begin my approach from the basics and move up to more complicated concepts in future posts.
The past few days I have began prototyping a grid-based pathfinding system.The idea originated from Rimworld, which uses a fairly large map and tens of agents, however I have added some more goals to spice things up:
The basic node creation code is this:
EDIT: Code updated Jul 14 2019.
And the pathfinding code is this:
Node resetting script (pf_find_cleanup):
I have used the Euclidean heuristic. The square root may seem slow, but contrary to what certain websites state, using the "square root free" version can actually botch the path since g and h will then be expressed in different metrics. In addition, the slow part will always be the large amount of explored nodes, calculating a cheaper heuristic doesn't make much of a difference. Finally, I want the very same algorithm to be used in HPA* (discussed later), where the Euclidean heuristic works best due to the spreading of abstract nodes.

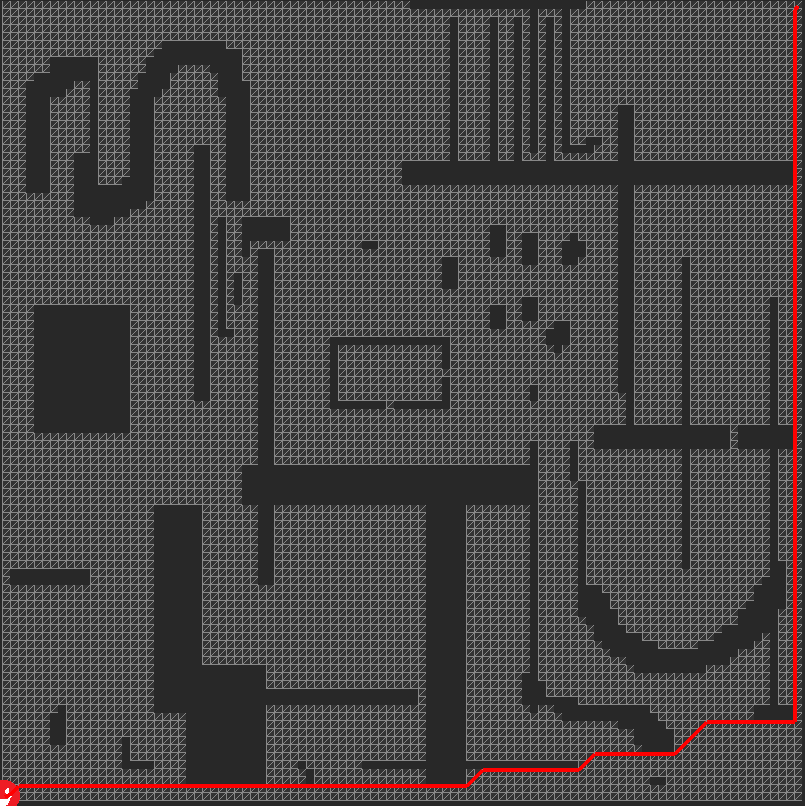
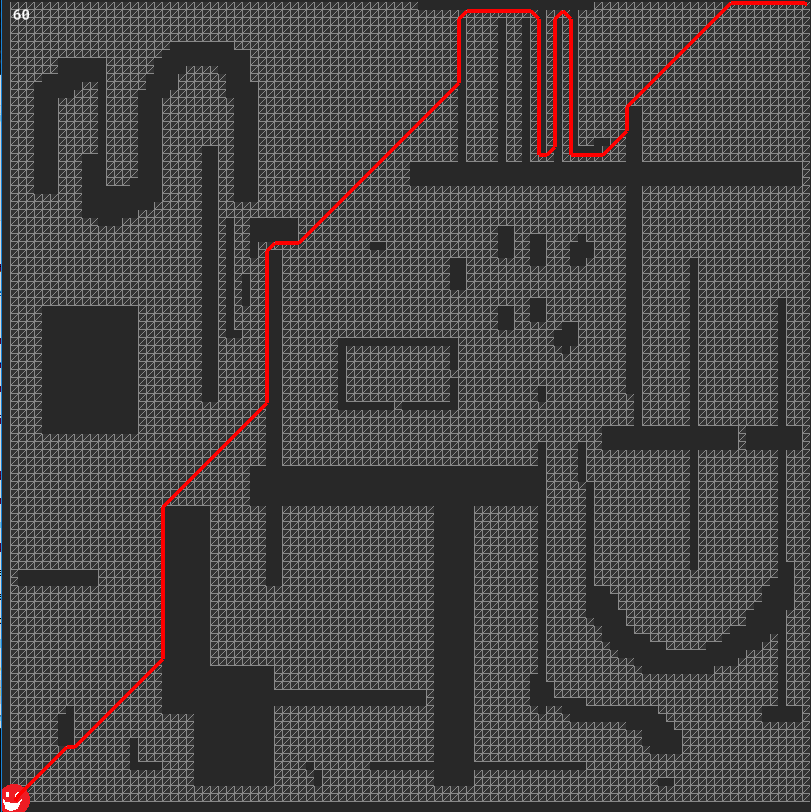
All tests are run in YYC. As you can see, the algorithm takes ~67 milliseconds on a 100x100 grid to reach a faraway point. The turquoise grid and blue dots you see in the screenshot are used in HPA*, ignore them for now. Also, The path list omits the last (goal) node for now, I will fix that later.
Obviously, 67 milliseconds for just a 100x100 map seems like a lot of time, it's definitely prohibitive for realtime calculation. Even if we split that up in multiple steps, it would still take some frames for an agent to start moving. I am trying to avoid such an approach if possible.
EDIT (Jul 14 2019): Same path is calculated in ~29 ms with the new code.
So I will leave you with this first post and add some questions for discussion:
This is mainly a discussion/presentation of ideas thread. There are lots of good pathfinding concepts and I am not pretending to know all about them. Hopefully this thread will grow to a meaningful exchange of knowledge. I will begin my approach from the basics and move up to more complicated concepts in future posts.
The past few days I have began prototyping a grid-based pathfinding system.The idea originated from Rimworld, which uses a fairly large map and tens of agents, however I have added some more goals to spice things up:
- Multiple grids of variable size and relative locations to each other. Agents will be able to "jump" from grid to grid if they are close enough. Imagine something like jumping from an asteroid to a nearby one with your jetpack.
- Portals/teleporters and/or muti-floor (like subterranean levels below ground)
- Variable-cost terrain
- Dynamically changing obstacles
- Speed-efficient. Ideally, agent pathfinding search should be queued (ie only a certain agent(s) during a step can calculate a new path)
- 8-directional movement
- Each node has a "list" flag indication which list it belongs to: Open, Closed or None.
- Used a priority list along with a normal list for the Open nodes. In this sense, the Open list is probably redundant but it helps when checking which list a node belongs to, since lists have always different indices, plus the Open list contents can be used later for cleanup/resetting explored nodes. I haven't tested if it will be as fast to cleanup from a priority list but I have my doubts.
The basic node creation code is this:
EDIT: Code updated Jul 14 2019.
Code:
/*
Argument0: grid id
Argument1: grid i
Argument2: grid j
*/
var array;
array[c_pfcost]=1;
array[c_pfgrid]=argument0;
array[c_pfi]=argument1;
array[c_pfj]=argument2;
array[c_pfg]=0;
array[c_pfh]=0;
array[c_pfparent]=-1;
array[c_pflist]=-1;
array[c_pfneighbor]=ds_list_create();
array[c_pfneighbordist]=ds_list_create();
ds_list_add(global.list_node_created,array);
return array;And the pathfinding code is this:
Code:
/*
Argument0: path list id
Argument1: start node
Argument2: end node
Argument3: (optional) left border
Argument4: (optional) top border
Argument5: (optional) right border
Argument6: (optional) bottom border
*/
var list_inode=argument[0];
var node_start=argument[1];
var node_end=argument[2];
var border_left=-infinity;
var border_right=infinity;
var border_top=-infinity;
var border_bottom=infinity;
if (argument_count>3) then {
border_left=argument[3];
border_top=argument[4];
border_right=argument[5];
border_bottom=argument[6];
}
var stack_cleanup=global.stack_cleanup;
var plist_open=global.pf_plist_open;
var endx=node_end[c_pfi];
var endy=node_end[c_pfj];
var list_child=global.pf_list_nodechild;
var list_childdist=global.pf_list_nodechilddist;
var tt=0,t1,t2;
var i,nodelist;
var node,node_current;
var size,tg,h;
var psize=1;
node_start[@c_pflist]=c_openlist;
ds_stack_push(stack_cleanup,node_start);
ds_priority_add(plist_open,node_start,0);
while (psize>0) {
node_current=ds_priority_delete_min(plist_open);
psize+=-1;
if (node_current==node_end) then {
while (node_current<>-1) {
ds_list_insert(list_inode,0,node_current);
node_current=node_current[c_pfparent];
}
pf_find_cleanup();
exit;
}
node_current[@c_pflist]=c_closedlist;
//pf_getneighbors(node_current,border_left,border_top,border_right,border_bottom);
list_child=node_current[c_pfneighbor];
list_childdist=node_current[c_pfneighbordist];
var xx,yy;
size=ds_list_size(list_child);
for (i=0;i<size;i+=1) {
node=list_child[|i];
xx=node[c_pfi]; yy=node[c_pfj];
if (xx>=border_left && xx<=border_right && yy>=border_top && yy<=border_bottom) then {
nodelist=node[c_pflist];
if (nodelist==c_closedlist) then {
continue;
} else {
tg=node_current[c_pfg] + (node[c_pfcost]*list_childdist[|i]);
if (nodelist==c_openlist) then {
if (tg<node[c_pfg]) then {
node[@c_pfg]=tg;
node[@c_pfparent]=node_current;
//h=max(abs(xx-endx),abs(yy-endy));
//ds_priority_change_priority(plist_open,node,(tg+h));
}
} else {
node[@c_pfg] = tg;
h=max(abs(xx-endx),abs(yy-endy));
node[@c_pfh] = h;
node[@c_pfparent] = node_current;
node[@c_pflist]=c_openlist;
ds_priority_add(plist_open,node,(tg+h));
ds_stack_push(stack_cleanup,node);
psize+=1;
}
}
}
}
}
pf_find_cleanup();Node resetting script (pf_find_cleanup):
Code:
var stack_cleanup=global.stack_cleanup;
var plist_open=global.pf_plist_open;
var node;
while ds_stack_size(stack_cleanup)>0 {
node=ds_stack_pop(stack_cleanup);
node[@c_pflist]=-1;
node[@c_pfparent]=-1;
}
ds_priority_clear(plist_open);I have used the Euclidean heuristic. The square root may seem slow, but contrary to what certain websites state, using the "square root free" version can actually botch the path since g and h will then be expressed in different metrics. In addition, the slow part will always be the large amount of explored nodes, calculating a cheaper heuristic doesn't make much of a difference. Finally, I want the very same algorithm to be used in HPA* (discussed later), where the Euclidean heuristic works best due to the spreading of abstract nodes.

All tests are run in YYC. As you can see, the algorithm takes ~67 milliseconds on a 100x100 grid to reach a faraway point. The turquoise grid and blue dots you see in the screenshot are used in HPA*, ignore them for now. Also, The path list omits the last (goal) node for now, I will fix that later.
Obviously, 67 milliseconds for just a 100x100 map seems like a lot of time, it's definitely prohibitive for realtime calculation. Even if we split that up in multiple steps, it would still take some frames for an agent to start moving. I am trying to avoid such an approach if possible.
EDIT (Jul 14 2019): Same path is calculated in ~29 ms with the new code.
So I will leave you with this first post and add some questions for discussion:
- Time-wise, is the algorithm I wrote efficient? 67 milliseconds looks like a lot, I suspect that e.g. in C++ it would be a lot less. Is my assumption true? Is YYC inherently slower, or have I made some undetectable mistake?
- Do you have to propose other optimisation concerning the "Vanilla" A* algorithm? I am not talking (yet) about other hybrid methods like hierarchical A* or Theta or JPS, I am still talking about the "bare-bones" A* code.
- If you have written your own A* pathfinding code, what were your own times, and how did you achieve them? Again, since this post covers only the A* approach, try to stick with A* for now.
Last edited: